Acceleration Due To Gravity

In older times, people used to think that the Earth was flat. Imagine that the Earth is indeed not a sphere of radius $R$, but an infinite plate of thickness $H$. What value of $H$ is needed to allow the same gravitational acceleration to be experienced as on the surface of the actual Earth? (Assume that the Earth's density is uniform and equal in the two models).

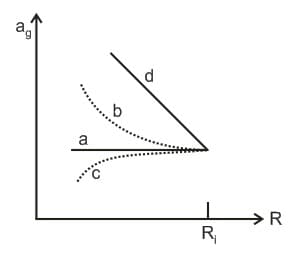
A (nonrotating) star collapses onto itself from an initial radius ${\text{R}}_{\text{i}}$ with its mass remaining unchanged. Which curve in figure best gives the gravitational acceleration ${\text{a}}_{\text{g}}$ on the surface of the star as a function of the radius of the star during the collapse?

If a tunnel is cut at any orientation through the earth, then a ball released from one end will reach the other end in how much time (neglect earth rotation)? 

The mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this planet if it is a second pendulum on earth?

If the radius of the earth be increased by a factor of 5, by what factor its density be changed to keep the value of g same?

Let $\omega$ be the angular velocity of the earth's rotation about its axis. Assume that the acceleration due to gravity on the earth's surface has the same value at the equator and the poles. An object weighed at the equator gives the same reading as a reading taken at a depth $\mathrm{d}$ below earth's surface at a pole $\left(d\ll R\right)$. The value of $d$ is:

A man is standing on an international space station, which is orbiting earth at an altitude $520 \mathrm{km}$ with a constant speed $7.6 \mathrm{km} {\mathrm{s}}^{-1}$. If the man's weight is $50 \mathrm{kg}$, his acceleration is

Two planets A and B of radii $R$ and $1.5 R$ have densities $\rho$ and $\frac{\rho }{2}$ respectively. The ratio of acceleration due to gravity at the surface of B to A is:

The radii of two planets $A$ and $B$ are $R$ and $4R$ and their densities are $\rho$ and $\frac{\rho }{3}$ respectively. The ratio of acceleration due to gravity at their surfaces $\left(g_A:g_B\right)$ will be
 

The weight of a body on the earth is $400 \mathrm{N}.$ Then weight of the body when taken to a depth half of the radius of the earth will be:

Assuming the earth to be a sphere of uniform mass density, the weight of a body at a depth $d=\frac{R}{2}$ from the surface of earth, if its weight on the surface of earth is $200 \mathrm{N}$, will be : (Given $R=$ radius of earth)

A planet has double the mass of the earth. Its average density is equal to that of the earth. An object weighing $W$ on earth will weigh on that planet:

The weight of a body on the surface of the earth is $100 \mathrm{N}$. The gravitational force on it when taken at a height, from the surface of earth, equal to one-fourth the radius of the earth is:

The acceleration due to gravity at height $h$ above the earth if $h\ll R$ (Radius of earth) is given by

An object weighs $200 \mathrm{N}$ at the surface of Earth. Find the weight at a depth of $\frac{R}{2}$, where $R$ is the radius of Earth.

Which of the following expression gives the value of acceleration due to gravity $g^{\text{'}}$ at the altitude $h$ above the surface of Earth.

($R=$radius of Earth, $g=$acceleration due to gravity at surface of Earth)

If the weight of an object on earth's surface is $400 \mathrm{N}$, then weight of the same particle at a depth $\frac{R}{2}$ from surface would be ($R$ is radius of earth)

If $W$ is the weight on the surface of Earth then weight of same body at a height $\frac{R_e}{4}$ above the surface of Earth is equal to

($R_e=$ Radius of Earth)

On a planet $\rho$(mass density) is same as that of Earth while mass of planet is twice than that of Earth. Ratio of weight of a body on surface of the planet to that on Earth is equal to:

Assuming that the earth is a sphere of radius $R_{E }$ with uniform density, the distance from its centre at which the acceleration due to gravity is equal to $\frac{g}{3}$ ($g$ is the acceleration due to gravity on the surface of earth) is